“Será possível conhecer?” – O Paradoxo do Mentiroso e a sua Relevância na Lógica (II)

Continuação de : “Será possível conhecer?” – O Paradoxo do Mentiroso e a sua Relevância na Lógica (I)
Autorreferência e Referência Circular
O paradoxo do mentiroso parece resultar, em parte, do facto de uma proposição poder predicar-se a si mesma. Neste sentido, uma possível solução poderia passar por descartar como inválidas todas as fórmulas linguísticas que apresentam autorreferência. No entanto, essa solução não é a mais viável pelas razões que a seguir se apresentam.
Ao considerarmos inválidas fórmulas linguísticas que apresentam autorreferência estamos a reduzir a expressividade da nossa linguagem lógica. Fórmulas linguísticas como as que se seguem não seriam proposições, nem portadoras de valor de verdade, apesar de ocorrerem na nossa linguagem natural: 𝑄:
𝑄 é 𝑢𝑚𝑎 𝑝𝑟𝑜𝑝𝑜𝑠𝑖çã𝑜.
𝑅:𝑅 é 𝑢𝑚𝑎 𝑝𝑟𝑜𝑝𝑜𝑠𝑖çã𝑜 𝑒𝑥𝑝𝑟𝑒𝑠𝑠𝑎 𝑝𝑜𝑟 𝑢𝑚𝑎 𝑓𝑟𝑎𝑠𝑒 𝑐𝑜𝑛𝑠𝑡𝑖𝑡𝑢í𝑑𝑎 𝑝𝑜𝑟 𝑜𝑛𝑧𝑒 𝑝𝑎𝑙𝑎𝑣𝑟𝑎𝑠.
O senso comum leva-nos a entender ambas as fórmulas linguísticas não só como proposições, mas como proposições verdadeiras.
Além disso, existem versões do paradoxo do mentiroso que não dependem de autorreferência, como o que se segue:
𝑃1:𝑃2 é 𝑢𝑚𝑎 𝑝𝑟𝑜𝑝𝑜𝑠𝑖çã𝑜 𝑣𝑒𝑟𝑑𝑎𝑑𝑒𝑖𝑟𝑎.
𝑃2:𝑃1 é 𝑢𝑚𝑎 𝑝𝑟𝑜𝑝𝑜𝑠𝑖çã𝑜 𝑓𝑎𝑙𝑠𝑎.
O sistema de proposições anterior também resulta em contradição. No entanto, apesar de não apresentar autorreferência, apresenta, como se constata, referência circular. A restrição da nossa linguagem lógica poderia estender-se, assim, a fórmulas lógicas que apresentam, para além de autorreferência, referência circular. No entanto, isso reduz ainda mais a expressividade da nossa linguagem lógica, ao tomar como inválidas situações de discurso como a seguinte:
𝐽𝑜ã𝑜:”Tudo o que o Pedro disse sobre mim é verdade”.
𝑃𝑒𝑑𝑟𝑜:”Tudo o que o João disse sobre mim também é verdade”
Novamente, o senso comum leva-nos a admitir situações de discurso como a anterior como coerentes e, se devidamente contextualizadas, como portadoras de sentido.
Além disso, o filósofo Stephen Yablo mostrou que é possível criar uma versão do paradoxo do mentiroso que não depende de referência circular, através de uma sequência infinita de proposições, às quais são atribuídas, por ordem, índices naturais. Nesta sequência, uma proposição de índice 𝑘∈ℕ afirma a falsidade de todas as proposições de índice maior do que o seu, isto é, de índice 𝑛∈ℕ,𝑛>𝑘. Por outras palavras, a proposição de índice 1 afirma a falsidade de todas as proposições com índice maior do que 1; a proposição de índice 2 afirma a falsidade de todas as proposições com índice maior do que 2; e assim sucessivamente, tal como se segue:
𝑃1:𝑃𝑎𝑟𝑎 𝑡𝑜𝑑𝑜 𝑛>1, 𝑃𝑛 é 𝑓𝑎𝑙𝑠𝑎.
𝑃2:𝑃𝑎𝑟𝑎 𝑡𝑜𝑑𝑜 𝑛>2, 𝑃𝑛 é 𝑓𝑎𝑙𝑠𝑎.
𝑃3:𝑃𝑎𝑟𝑎 𝑡𝑜𝑑𝑜 𝑛>3, 𝑃𝑛 é 𝑓𝑎𝑙𝑠𝑎.
Para entender o paradoxo, vamos atribuir um valor de verdade a “P1”. Admitindo que “P1” é verdadeira, então todas as proposições com índice maior do que 1 são falsas, nomeadamente a proposição “P2”. Se a proposição “P2” é falsa, então a sua negação é verdadeira, isto é, é verdadeira a proposição «Existe pelo menos um 𝑛>2 para o qual “Pn” é verdadeira». Logo, podemos admitir que a proposição “Pi”, onde 𝑖>2, é verdadeira. No entanto, como 𝑖>1, então “Pi” é, segundo “P1”, que admitimos ser verdadeira, falsa, o que constitui uma contradição. Para clarificar o paradoxo, construímos o seguinte diagrama:
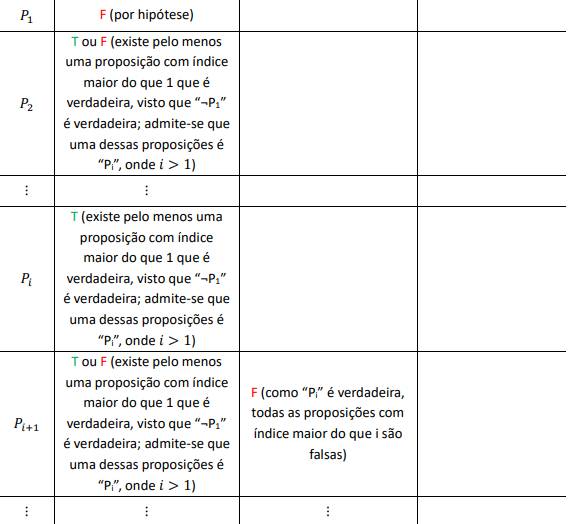
Como a hipótese resultou em absurdo, vamos admitir que “P1” é falsa. Se a proposição “P1” é falsa, então a sua negação é verdadeira, isto é, é verdadeira a proposição «Existe pelo menos um 𝑛>1 para o qual “Pn” é verdadeira». Logo, podemos admitir que a proposição “Pi”, onde 𝑖>1, é verdadeira. Mas o que diz a proposição “Pi”? Diz que «Para todo 𝑛>𝑖, “Pn” é falsa». Logo, de acordo com “Pi”, como 𝑖+1>𝑖, então “Pi+1” é falsa, pelo que a sua negação é verdadeira, isto é, é verdadeira a proposição «Existe pelo menos um 𝑛>𝑖+1 para o qual “Pn” é verdadeira». Logo, podemos admitir que a proposição “Pj”, onde 𝑗>𝑖+1, é verdadeira. No entanto, como 𝑗>𝑖, então “Pj” é, segundo “Pi”, que admitimos ser verdadeira, falsa, o que constitui uma contradição. Para clarificar o paradoxo, podemos recorrer novamente ao diagrama:
Como é possível observar, extinguir autorreferência e referência circular de uma linguagem não permite resolver o paradoxo do mentiroso.